Hi Folks,
The n-queen’s problem says that on an n x n chessboard, there cannot be queens in the same column, row, or diagonal. Here’s one solution to the n-queen’s problem for a 4 x 4 board:
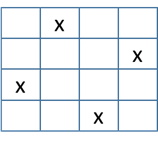
One way to model the n-queen’s problem is to have an element for each column, whose contents is the row that its queen is located on. For example, this XML instance represents the above board:
<n-queens>
<column1><row>3</row></column1>
<column2><row>1</row></column2>
<column3><row>4</row></column3>
<column4><row>2</row></column4>
</n-queens>
Below is a Schematron schema that constrains XML instances to valid solutions of the n-queen’s problem. It’s a brute-force implementation. Is there is a more flexible implementation? /Roger
<sch:schema
xmlns:sch="http://purl.oclc.org/dsdl/schematron"
queryBinding="xslt2">
<sch:pattern
id="n-Queens-Problem">
<sch:rule
context="n-queens">
<sch:assert
test="count(distinct-values(//row))
eq 4">
There cannot be a queen on the same row.
</sch:assert>
</sch:rule>
<sch:rule
context="column1">
<sch:assert
test="
number(../column2/row) ne (row + 1) and
number(../column3/row) ne (row + 2) and
number(../column4/row) ne (row + 3) and
number(../column2/row) ne (row - 1) and
number(../column3/row) ne (row - 2) and
number(../column4/row) ne (row - 3)
">
There cannot be a queen diagonal to the queen in column1.
</sch:assert>
</sch:rule>
<sch:rule
context="column2">
<sch:assert
test="
number(../column3/row) ne (row + 1) and
number(../column4/row) ne (row + 2) and
number(../column3/row) ne (row - 1) and
number(../column4/row) ne (row - 2)
">
There cannot be a queen diagonal to the queen in column2.
</sch:assert>
</sch:rule>
<sch:rule
context="column3">
<sch:assert
test="
number(../column4/row) ne (row + 1) and
number(../column4/row) ne (row - 1)
">
There cannot be a queen diagonal to the queen in column3.
</sch:assert>
</sch:rule>
</sch:pattern>
</sch:schema>

